Presentation Information
[O16-3]Graph Neural Networks to Predict Coercivity of Hard Magnetic Microstructures
*Heisam Adam Moustafa1, Qais Ali2, Leonie Breth1, Alexander Kovacs1, Thomas Schrefl1,2, Lukas Fink3, William Rigaut3, Pierre Le-Berre3, Thibaut Devillers3, Nora M. Dempsey3, Harald Oezelt1 (1. Department for Integrated Sensor Systems, University for Continuing Education Krems (Austria), 2. Christian Doppler Laboratory for magnet design through physics informed machine learning (Austria), 3. Université Grenoble Alpes, CNRS, Grenoble INP, Institut Néel (France))
Keywords:
Graph Neural Network,Machine Learning,Micromagnetism
With the dramatic progress of climate change, the green energy transition is more urgently needed than ever. Permanent magnets, containing rare earth elements (REE), are used in many technologies, e.g., wind turbines, electric vehicles, which drive this transition. The use of the heavy REE dysprosium, for example, is predicted to rise more than fivefold by 2050 [1]. Given the ecological and economic importance of REE, it is crucial to use them selectively and only where absolutely necessary in permanent magnets to mitigate supply risks while maintaining the magnet’s performance. A promising strategy to achieve this goal is micro- and nanostructural design [2] [3].
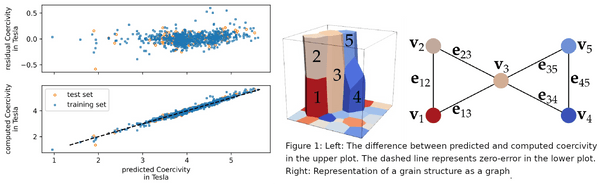
To reduce the computational effort of micromagnetic simulations, which provide a tool to examine the impact of different microstructures on the permanent magnets performance, we developed a graph neural network (GNN). GNNs are specific artificial neural networks, which operate on graph-structured data. GNNs have been applied to predict properties of polycrystalline materials and outperformed linear regression and CNN models [4]. Their message passing and convolution abilities, enable to mimic the real world micromagnetic behavior of short- and long-range interactions among the grains or grain boundaries, such as magneto-statics. In a polycrystalline hard magnetic structure, the nodes represent individual grains, while the edges correspond to the grain boundaries.
We generated a heterogeneous dataset of over 1000 polycrystalline NdFeB cubic microstructures to train and evaluate the GNN. The polycrystal structure was obtained from Neper [5], meshed using salome [6], and its hysteresis curve calculated using our reduced order model (ROM) [7]. With the help of feature correlation analysis and empirical observation, 12 node features and the grain boundary thickness as an edge feature were selected. The coercive field, an important measure of a magnet’s performance, was extracted from the computed hysteresis curves and used as the target variable for the graph-level regression. The dataset is split up into a training-, validation-, and test-set with the ratio 70/15/15. Scaling is applied to the node features, to prevent certain features dominating others.
The GNNs first linear layer is an embedding layer, to transform the node features into a higher dimensional space, enabling the capture of more complex relationships. Two custom convolutional layers, inspired by [5], aggregate information from neighboring grains and hence capture long-range interactions. These are followed by a dense layer with dropout for regularization and a global mean pooling layer for the graph-level regression task. The final 10 hidden layers and three dense layers enhance the model's ability to capture complex relationships.
The hyperparameters of the GNN model, such as the number of convolutional layers, were tuned using a grid search.
To demonstrate the GNNs out-of-distribution (OOD) prediction abilities, the network was trained on microstructures with smaller edge lengths and evaluated on larger structures. The developed GNN shows an excellent accuracy when predicting coercivity, demonstrated by a R² value of 97% for the test set. For OOD prediction the R² value of the test set is 85%, which is still satisfactory. In further work, we aim to improve generalization capabilities and implement node-level regression to predict the whole hysteresis curve.
This research was funded in whole or in part by the Austrian Science Fund (FWF) I 6159-N and the French National Research Agency ANR-22-CE91-0008.
[1] European Commission, Critical Raw Materials, 2020.
[2] R. Skomski, J. Coey, Scripta Mater. 112 (2016) 3–8.
[3] N. Poudyal, J. P. Liu, J. Phys. D: Appl. Phys. 46 (2013) 043001.
[4] M. Dai et al., Comput. Mater. Sci. 230 (2023) 112461.
[5] R. Quey et al., Comput. Methods Appl. Mech. Eng. 200 (2011) 1729–1745.
[6] Salome Team, SALOME Software, 2021.
[7] H. Moustafa et al., AIP Adv. 14 (2024) 025001.
To reduce the computational effort of micromagnetic simulations, which provide a tool to examine the impact of different microstructures on the permanent magnets performance, we developed a graph neural network (GNN). GNNs are specific artificial neural networks, which operate on graph-structured data. GNNs have been applied to predict properties of polycrystalline materials and outperformed linear regression and CNN models [4]. Their message passing and convolution abilities, enable to mimic the real world micromagnetic behavior of short- and long-range interactions among the grains or grain boundaries, such as magneto-statics. In a polycrystalline hard magnetic structure, the nodes represent individual grains, while the edges correspond to the grain boundaries.
We generated a heterogeneous dataset of over 1000 polycrystalline NdFeB cubic microstructures to train and evaluate the GNN. The polycrystal structure was obtained from Neper [5], meshed using salome [6], and its hysteresis curve calculated using our reduced order model (ROM) [7]. With the help of feature correlation analysis and empirical observation, 12 node features and the grain boundary thickness as an edge feature were selected. The coercive field, an important measure of a magnet’s performance, was extracted from the computed hysteresis curves and used as the target variable for the graph-level regression. The dataset is split up into a training-, validation-, and test-set with the ratio 70/15/15. Scaling is applied to the node features, to prevent certain features dominating others.
The GNNs first linear layer is an embedding layer, to transform the node features into a higher dimensional space, enabling the capture of more complex relationships. Two custom convolutional layers, inspired by [5], aggregate information from neighboring grains and hence capture long-range interactions. These are followed by a dense layer with dropout for regularization and a global mean pooling layer for the graph-level regression task. The final 10 hidden layers and three dense layers enhance the model's ability to capture complex relationships.
The hyperparameters of the GNN model, such as the number of convolutional layers, were tuned using a grid search.
To demonstrate the GNNs out-of-distribution (OOD) prediction abilities, the network was trained on microstructures with smaller edge lengths and evaluated on larger structures. The developed GNN shows an excellent accuracy when predicting coercivity, demonstrated by a R² value of 97% for the test set. For OOD prediction the R² value of the test set is 85%, which is still satisfactory. In further work, we aim to improve generalization capabilities and implement node-level regression to predict the whole hysteresis curve.
This research was funded in whole or in part by the Austrian Science Fund (FWF) I 6159-N and the French National Research Agency ANR-22-CE91-0008.
[1] European Commission, Critical Raw Materials, 2020.
[2] R. Skomski, J. Coey, Scripta Mater. 112 (2016) 3–8.
[3] N. Poudyal, J. P. Liu, J. Phys. D: Appl. Phys. 46 (2013) 043001.
[4] M. Dai et al., Comput. Mater. Sci. 230 (2023) 112461.
[5] R. Quey et al., Comput. Methods Appl. Mech. Eng. 200 (2011) 1729–1745.
[6] Salome Team, SALOME Software, 2021.
[7] H. Moustafa et al., AIP Adv. 14 (2024) 025001.