Presentation Information
[O16-4]Optimization of a Permanent Magnet with Uncertainty Control
*Clemens Wager1, Thomas Schrefl1,2, Alexander Kovacs2, Harald Özelt2, Claas Fillies2, Qais Ali1, Felix Lasthofer2, Masao Yano3, Noritsugu Sakuma3, Akihito Kinoshita3, Tetsuya Shoji3, Akira Kato3, Hayate Yamano3 (1. Christian Doppler Laboratory for magnet design through physics informed machine learning (Austria), 2. Department of Integrated Sensor Systems, University for Continuing Education Krems, Wiener Neustadt, Austria (Austria), 3. Advanced Materials Engineering Division, Toyota Motor Corporation, Susono, Japan (Japan))
Keywords:
Optimization,Machine Learning,Uncertainty,Coercivity,Heavy Rare Earth Elements
Coercivity is one of the most important extrinsic properties in permanent magnets and strongly influenced by its microstructure. Yet the relationship between coercivity and microstructure remains in need of further exploration. [1]
We optimize the chemical composition of a (Nd,Ce,La,Pr,Tb,Dy)2(Fe,Co,Ni)14(B,C) permanent magnet maximizing coercivity and minimizing material cost. To account for the microstructure, we use Kronmüller’s equation [2] where the coercive field Hc is a function of the anisotropy field (Ha), saturation magnetization (Ms), misalignments and surface defects parameter alpha and effective demagnetization factor Neff [3]. The basis for this study is a database of many different 2-14-1 permanent magnet’s chemical composition and their corresponding Ha and Ms measured at different temperatures.
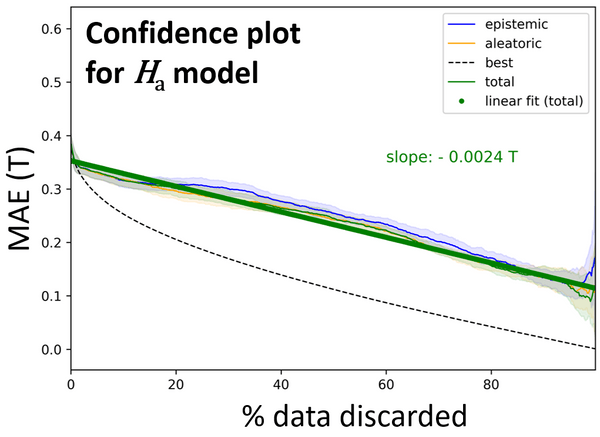
The design space is explored using a genetic algorithm, NSGA-II [4]. This optimization algorithm calls a set of Bayesian neural network [5] regressors trained on our database as objective functions. These predictors predict the material cost, Ha and Ms of an input chemical composition. Additionally, we obtain an uncertainty estimate with each predicted value. We can split the uncertainty into two main types: Aleatoric uncertainty, stems from the inherent noise in the data, and epistemic uncertainty, stems from a lack of knowledge about the system being modeled [6]. Figure 1 illustrates how we evaluate the model’s uncertainty estimate. During genetic optimization we remove solutions from the algorithm’s population which have an uncertainty greater than 15% in the anisotropy field or the magnetization controlled via constraints.
We investigate the change in Pareto frontiers for different misalignments, defects, demagnetization effects and temperature conditions by fixing alpha and Neff value in Kronmüller’s equation. Our findings suggest that the heavy rare earth content must be increased to reach the same coercive field for increased Neff and temperature.
In this research we focus on permanent magnets that may find application in electric motors where an operating temperature of 453 K is expected and a coercivity of at least 1.5 T is required. For example, our optimization scheme predicts that the least expensive chemical composition for a permanent magnet meeting these requirements with the fixed microstructural parameters alpha=0.45 and an Neff=1.22 is
(Nd0.58La0.42)2Fe14B0.42C0.58. Our study further demonstrates how to control uncertainty from machine learning predictions effectively, which is especially important when predicting out of sample. With good uncertainty estimates we can identify unreliable predictions and focus experimental efforts on the most promising candidate materials.
Figure 1: Confidence curves for the aleatoric uncertainty in yellow, the epistemic uncertainty in blue, and the total uncertainty for prediction of anisotropy field in green. The curves show the mean absolute error as function of the percentage of data discarded from the test set ranked by predicted uncertainty. The error scores where averaged over prediction on ten randomly chosen test data splits. The shaded areas denote the standard deviation. The black dashed line is the oracle confidence curve, which represents the ideal scenario where a model's uncertainty estimates perfectly align with the true errors in its predictions.
References:
[1] Li J, Sepehri-Amin H, Sasaki T, et al. Sci Technol Adv Mater., Vol. 22, p. 386 (2021)
[2] Kronmüller H, Durst KD, Sagawa M. J. Magn. Magn. Mater., 74, p. 291–302 (1988)
[3] Bance S, Seebacher B, Schrefl T, et al. J. Appl. Phys., Vol. 116 (2014)
[4] Deb K, Pratap A, Agarwal S, et al., IEEE Transactions on Evolutionary Computation, Vol. 6, p. 182 (2002)
[5] Gal Y, Ghahramani Z. In Proceedings of The 33rd International Conference on Machine Learning; PMLR, pp 1050-1059 (2016)
[6] Lakshminarayanan B, Pritzel A, Blundell C. Advances in neural information processing systems (2017)
We optimize the chemical composition of a (Nd,Ce,La,Pr,Tb,Dy)2(Fe,Co,Ni)14(B,C) permanent magnet maximizing coercivity and minimizing material cost. To account for the microstructure, we use Kronmüller’s equation [2] where the coercive field Hc is a function of the anisotropy field (Ha), saturation magnetization (Ms), misalignments and surface defects parameter alpha and effective demagnetization factor Neff [3]. The basis for this study is a database of many different 2-14-1 permanent magnet’s chemical composition and their corresponding Ha and Ms measured at different temperatures.
The design space is explored using a genetic algorithm, NSGA-II [4]. This optimization algorithm calls a set of Bayesian neural network [5] regressors trained on our database as objective functions. These predictors predict the material cost, Ha and Ms of an input chemical composition. Additionally, we obtain an uncertainty estimate with each predicted value. We can split the uncertainty into two main types: Aleatoric uncertainty, stems from the inherent noise in the data, and epistemic uncertainty, stems from a lack of knowledge about the system being modeled [6]. Figure 1 illustrates how we evaluate the model’s uncertainty estimate. During genetic optimization we remove solutions from the algorithm’s population which have an uncertainty greater than 15% in the anisotropy field or the magnetization controlled via constraints.
We investigate the change in Pareto frontiers for different misalignments, defects, demagnetization effects and temperature conditions by fixing alpha and Neff value in Kronmüller’s equation. Our findings suggest that the heavy rare earth content must be increased to reach the same coercive field for increased Neff and temperature.
In this research we focus on permanent magnets that may find application in electric motors where an operating temperature of 453 K is expected and a coercivity of at least 1.5 T is required. For example, our optimization scheme predicts that the least expensive chemical composition for a permanent magnet meeting these requirements with the fixed microstructural parameters alpha=0.45 and an Neff=1.22 is
(Nd0.58La0.42)2Fe14B0.42C0.58. Our study further demonstrates how to control uncertainty from machine learning predictions effectively, which is especially important when predicting out of sample. With good uncertainty estimates we can identify unreliable predictions and focus experimental efforts on the most promising candidate materials.
Figure 1: Confidence curves for the aleatoric uncertainty in yellow, the epistemic uncertainty in blue, and the total uncertainty for prediction of anisotropy field in green. The curves show the mean absolute error as function of the percentage of data discarded from the test set ranked by predicted uncertainty. The error scores where averaged over prediction on ten randomly chosen test data splits. The shaded areas denote the standard deviation. The black dashed line is the oracle confidence curve, which represents the ideal scenario where a model's uncertainty estimates perfectly align with the true errors in its predictions.
References:
[1] Li J, Sepehri-Amin H, Sasaki T, et al. Sci Technol Adv Mater., Vol. 22, p. 386 (2021)
[2] Kronmüller H, Durst KD, Sagawa M. J. Magn. Magn. Mater., 74, p. 291–302 (1988)
[3] Bance S, Seebacher B, Schrefl T, et al. J. Appl. Phys., Vol. 116 (2014)
[4] Deb K, Pratap A, Agarwal S, et al., IEEE Transactions on Evolutionary Computation, Vol. 6, p. 182 (2002)
[5] Gal Y, Ghahramani Z. In Proceedings of The 33rd International Conference on Machine Learning; PMLR, pp 1050-1059 (2016)
[6] Lakshminarayanan B, Pritzel A, Blundell C. Advances in neural information processing systems (2017)